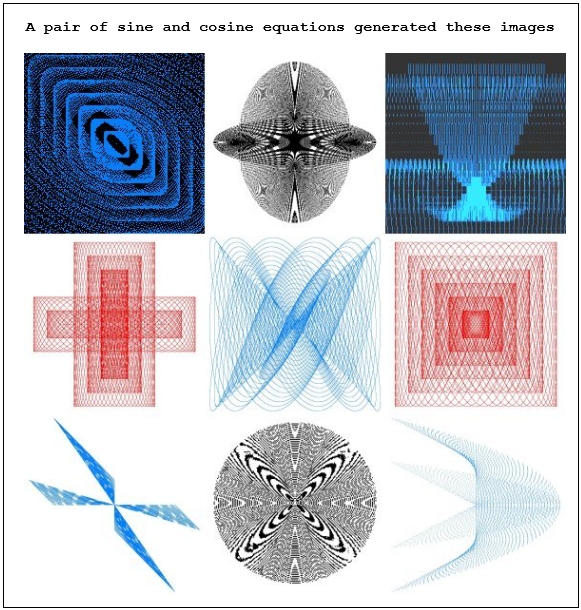
Iterated trigonometric equations with program code 
and graphical output by Roger Luebeck © 2017

Simple trig

Simple trig


    For C = 1 To iterations
    
    xangle = xangle + xinc
    yangle = yangle + yinc
    
    RN1 = RN1 + xinc: If RN1 > 1 Then RN1 = 0
    RN2 = RN2 + yinc: If RN2 > 1 Then RN2 = 0
    
    X = RN1 * (Cos(xangle) * ra) + 400
    Y = RN2 * (Sin(yangle) * ra) + 400
          
    viewport.PSet (X, Y), RGB(rd, gn, bl)

    Next C

I played a hunch and came up with an algorithm
for a pair of iterated trig equations, with
offsetting scalar multipliers for each equation.  
Elaborate patterns appeared which went way beyond
what I could have imagined. 

This program plots the sine of an incremently
increasing angle and the cosine of an incremently
increasing angle on the same graph.  The user has 
the option of making those increments the same or 
different.

The user can also specify whether the scalar
multiplier is the same or different for the two
equations.

The most interesting patterns are generated when
the increments are the same or extremely close
to the same.  Offsetting the scalar multipliers 
affects the symmetry in interesting ways.

40,000 to 1,000,000 iterations are typically
optimum.

The complete Visual BASIC program code is displayed 
further down.

(02/04/17 update:  I've just begun generating 3D images 
of these trig functions, which automatically have even 
more complex shapes.  Great stuff.  Some of the images
have been included at the bottom of this page.)

First up, are some spheres with various parameters.

Further down, are displayed some very surprising
images -- squares, triangles, spirals, and a host
of shapes that defy classification.




A couple half size images using different parameters:

  3D version images

Here are some 3D images.

My Visual BASIC program code: (2D)  (3D further down)

Private Sub trigrunbtn_Click()

iter = Val(iterbox.Text)
xinc = Val(xincbox.Text) * (3.14159265358979 / 180)
yinc = Val(yincbox.Text) * (3.14159265358979 / 180)
RN1 = Val(rn1box.Text)
RN2 = Val(rn2box.Text)

  
    For C = 1 To iter
    
    xangle = xangle + xinc
    yangle = yangle + yinc
    
    RN1 = RN1 + xinc: If RN1 > 1 Then RN1 = 0
    RN2 = RN2 + yinc: If RN2 > 1 Then RN2 = 0
    
    X = RN1 * (Cos(xangle) * 380) + 400 'or sine sine
    Y = RN2 * (Sin(yangle) * 380) + 400  
          
    viewport.PSet (X, Y), RGB(redd, greenn, bluee)

    Next C

End Sub

------------

My Visual BASIC program code: (3D)
(Includes rotation of image around all three axes)

Private Sub trigrunbtn_Click()

iter = Val(iterbox.Text)

xinc = Val(xincbox.Text) * (3.14159265358979 / 180)
yinc = Val(yincbox.Text) * (3.14159265358979 / 180)
zinc = Val(zincbox.Text) * (3.14159265358979 / 180)

RN1 = Val(rn1box.Text)
RN2 = Val(rn2box.Text)
RN3 = Val(rn3box.Text)

RX = RX * (3.14159 / 180)
RY = RY * (3.14159 / 180)
RY = RZ * (3.14159 / 180)

    For C = 1 To iter
    
    xangle = xangle + xinc
    yangle = yangle + yinc
    zangle = zangle + zinc
    
    RN1 = RN1 + R1INC: IF RN1 > 1 THEN RN1 = 0
    RN2 = RN2 + R2INC: IF RN2 > 1 THEN RN2 = 0
    RN3 = RN3 + R3INC: IF RN3 > 1 THEN RN3 = 0
    
    X = RN1 * SIN(XANGLE)
    Y = RN2 * COS(YANGLE)
    Z = RN3 * COS(ZANGLE)

    Y1 = (Y * COS(RX)) - (Z * SIN(RX))
    Z1 = ((Y * SIN(RX)) + (Z * COS(RX)))
    X1 = X

    Z2 = ((Z1 * COS(RY)) - (X1 * SIN(RY)))
    X2 = (Z1 * SIN(RY)) + (X1 * COS(RY))
    Y2 = Y1

    X3 = (X2 * COS(RZ)) - (Y2 * SIN(RZ))
    Y3 = (X2 * SIN(RZ)) + (Y2 * COS(RZ))
    Z3 = Z2
    
    GX = (((3.9 * X3) / (4 - Y3)) * RA) + 320
    GZ = -(((3.9 * Z3) / (4 - Y3)) * RA) + 260
         
    viewport.PSet (GX, GY), RGB(redd, greenn, bluee)

    Next C

End Sub


====================================================

home


Balloting

Simple trig

Logistic map

The Attractor of Henon

Number doubling

Barnsley's Fern

The Sierpinski Triangle